Data source and processing
In this section, we explain the in-store trajectory tracking experiment based on ILS using RFID, as shown in Fig. 9. Our ILS is equipped in a daily supermarket near out-of-town residences, and the experimental period is carried out over one month and one week. Since the in-store trajectory can only be tracked via RFID tags attached to shopping carts (see Fig. 9a), customers' purchases are therefore considered experimental targets. Customers' location information is collected and sent to the back-end data center (see Fig. 9b).
However, raw RFID data is different from mapping the current coordinates of the supermarket layout. The ILS provides a transformation process for changing location data as pixels of the layout image. Figure 10 shows the structure of a supermarket X And Y denotes the horizontal and vertical axes of the image pixels and O denotes the coordinate origin. According to the actual arrangement, we select three typical areas as experimental zones.
-
1.
Zone (F). There are three island shelves in this zone where customers go shopping in walking routes.
-
2.
Zone (G). In this zone there is only one straight path for customers to shop without any obstacles.
-
3.
Zone (M). In this zone there is only one island shelf where customers shop in a ribbon pattern.
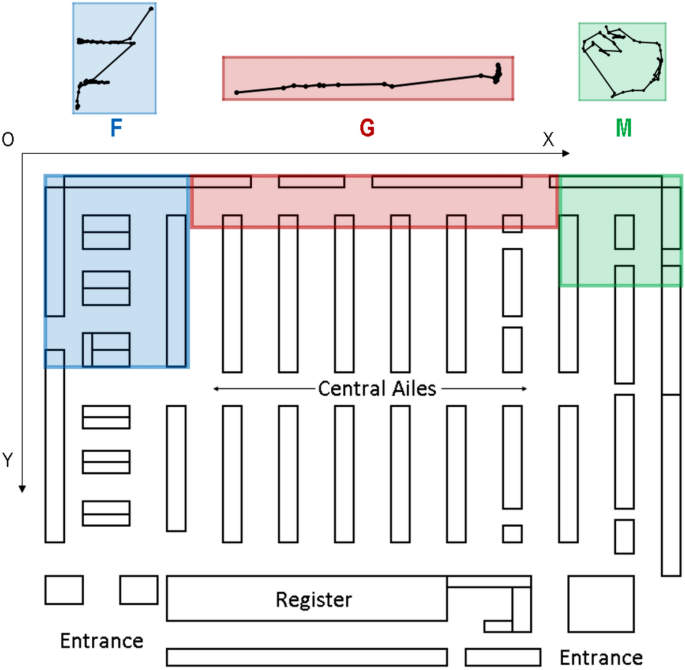
Store layout and experimental area.
The experimental data explanations of three samples are listed in Table 1. In each sample, we select 15,000 datasets, where 70% of the data is selected as training data, 10% of the data is assigned as validation data, and the remaining 20% is left. are used as test data for model validation.
Evaluation criterion
In model development, mean absolute error (MAE), mean absolute percentage error (MAPE), and root mean square error (RMSE) are used in this article.
$$\begin{aligned} MAE= & \frac{1}{n} \sum _{i=1}^{n} |y'_i – y_i| \end{aligned}$$
(22)
$$\begin{aligned} MAPE= & \frac{100\%}{n} \sum _{i=1}^{n} |\frac{y'_i – y_i}{y_i}| \end{aligned}$$
(23)
$$\begin{aligned} RMSE= & \sqrt{\frac{1}{n} \sum _{i=1}^{n} (y'_i – y_i)^2} \end{aligned}$$
(24)
where notations \(y'_i\) And \(y_i\) denote predicted and actual values and N denotes the total number.
In addition, the R-squared indicator (\(R^2\)) is also included, as in Eq. (25)
$$\begin{aligned} R^2 = 1- \frac{RSS}{TSS} \end{aligned}$$
(25)
And RSS, TSS denote the remaining sum of squares and the total sum of squares as follows.
$$\begin{aligned} RSS= & \sum _{i=1}^{n} (y_i – y'_i)^2 \end{aligned}$$
(26)
$$\begin{aligned} TSS= & \sum _{i=1}^{n} (y_i – \bar{y})^2 \end{aligned}$$
(27)
where notations \(y'_i\) And \(\bar{y}\) denote the predicted value and the average value of N Samples.
Results and comparisons
Parameter setting and value optimization
In experiments, we use 11 baseline models and 3 proposed models as comparisons. The comparison models include traditional models (e.g. SVM, MLP and BPNN) and classic RNN including its new variants (e.g. LSTM, GRU, Bi-LSTM and CNN-LSTM). The comparisons also include SOTA models such as Seq2Seq and two models of ST-LSTM and ResLSTM, which were not applied in predicting the in-store trajectory. These models and their parameters are described as follows.
-
1.
Classical regression analysis based on SVM uses parameters of the kernel function (F) and penalty coefficient (C)26.
-
2.
MLP-based linear regression analysis uses hidden state dimension parameters (\(d_{\mathrm{MLP}}\))27.
-
3.
Classic NN based on backpropagation (BPNN) uses hidden state dimension parameters (\(d_{\mathrm{BPNN}}\))28.
-
4.
Standard RNN uses hidden state dimension parameters (\(d_{\mathrm{RNN}}\))29.
-
5.
Standard LSTM uses hidden state dimension parameters (\(d_{\mathrm{LSTM}}\))30.
-
6.
Standard GRU uses hidden state dimension parameters (\(d_{\mathrm{GRU}}\))31.
-
7.
Bidirectional LSTM (BiLSTM) uses hidden state dimension parameters (\(d_{\mathrm{BiLSTM}}\))25.
-
8.
CNN-LSTM uses kernel size parameters \(K_{\mathrm{CNN}}\) and hidden state dimension (\(d_{\mathrm {CNN-LSTM}}\))32.
-
9.
Default Seq2Seq uses hidden state dimension parameters (\(d_{\mathrm{Seq2Seq}}\))7.
-
10.
Spatiotemporal LSTM (ST-LSTM) uses hidden state dimension parameters (\(d_{\mathrm {ST-LSTM}}\))33.
-
11.
Residual LSTM (ResLSTM) uses hidden state dimension parameters (\(d_{\mathrm{ResLSTM}}\))34.
The proposed models and their parameters are described as follows.
-
1.
The proposed LSTM-J uses hidden state dimension parameters (\(d_{\mathrm {LSTM-J}}\)).
-
2.
The proposed GRU-K uses hidden state dimension parameters (\(d_{\mathrm {GRU-K}}\)).
-
3.
Hybrid Recurrent Network (HRN) based on LSTM-J and GRU-K uses hidden state dimension parameters (\(d_{\mathrm{HRN}}\)).
In addition, in order to effectively capture trajectory changes while balancing computational efficiency and prediction accuracy, several experiments were conducted and the sliding window length (i.e., the input observation data) was set to 3 for all models used in the experiments. The parameter setting range and optimal value of each model are shown in Table 2.
Model comparisons and result analyses
In this section, we study and compare the prediction performance of in-store trajectory between proposed models and baseline models. After determining the optimal parameters for the training data shown in Table 2, the experimental results in this section are all based on test data. Fig. 11a–I present the errors of MAE, MAPE and RMSE between predicted and actual positions (X, j) of the trajectory. Since the trajectory prediction is a classic regression prediction, Fig. 11j-l show the \(\hbox {R}^2\) Comparison between predicted and actual positions. The results show that the proposed LSTM-J, GRU-K and HRN(LSTM-J, GRU-K) are sufficiently superior to other baseline models in MAE, RMSE, MAPE and \(\hbox {R}^2\) in zones F, G and M.
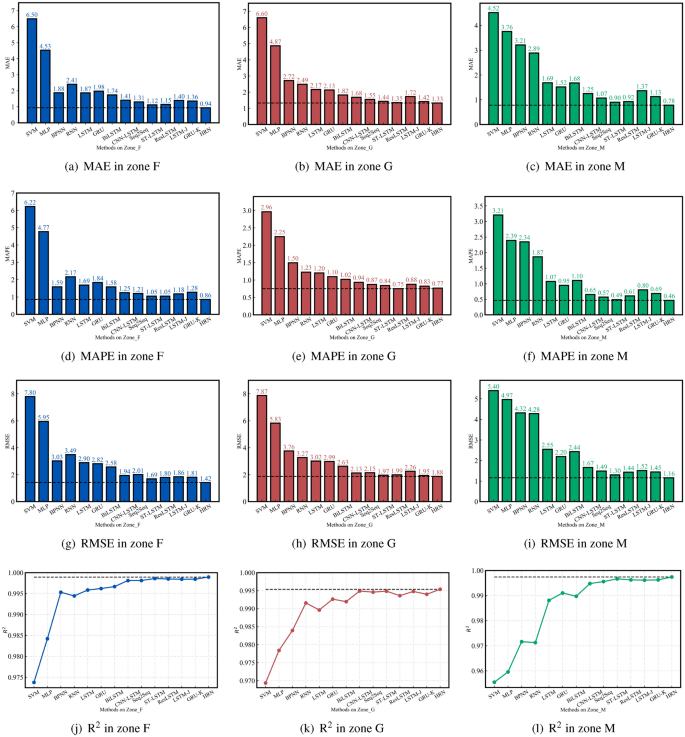
Rating comparisons of different models in three zones.
The quantitative results are presented in Table 3 and the summaries of the analyzes are described as follows.
-
(1)
The NNs including gate units can achieve better prediction performance than traditional NNs (MLP, BPNN, RNN) and SVM. The MAE, RMSE, MAPE and \(\hbox {R}^2\) Each one shows significant improvements across the three datasets, representing increases of 56.93%, 55.29%, 56.34%, and 1.84%, respectively.
-
(2)
The newly proposed gate unit NNs (LSTM-J, GRU-K) can achieve better prediction performance than existing gate unit NNs (LSTM, GRU) and variants (BiLSTM, CNN-LSTM). The MAE, RMSE, MAPE and \(\hbox {R}^2\) The metrics were improved for the 18.63%, 25.98%, 19.39%, and 0.31% datasets, respectively.
-
(3)
The proposed HRN consisting of LSTM-J and GRU-K can achieve better prediction performance than SOTA Seq2Seq, ST-LSTM, ResLSTM and even single LSTM-J or GRU-K. The corresponding MAE, RMSE, MAPE and \(\hbox {R}^2\) The values increased by 22.69%, 14.93%, 23.86% and 0.10%, respectively.
-
(4)
The proposed LSTM-J, GRU-K and HRN models can significantly improve the prediction of in-store shopping trajectories and show sufficient generalization for different types of shopping trajectories instead of all comparison models. Compared to all other models, the three models showed an average improvement of 30.20%, 34.68%, 30.26% and 0.85% in MAE, RMSE, MAPE and \(\hbox {R}^2\)respectively.
Model validations and performance discussions
In this section, we validate and demonstrate the effects of time step, epoch, and batch size on the model performance of the proposed LSTM-J, GRU-K, and HRN. The first validation is to examine the relationships between time steps and model performance. Here we set the time step to {2, 3, 4, 5} for three experimental zones as shown in Table 4. Figure 12, and examine the results of MAE, RMSE, MAPE and \(\hbox {R}^2\)respectively. In Table 4, the results of step = 2 in each zone are highlighted for lower and higher model errors, respectively \(\hbox {R}^2\) scores more points than other time steps, and at the same time, the results of HRN are highlighted due to its best performance on all patterns under the same conditions (except the MAPE situation in zone F with step = 5). Therefore, the performance of time step can be shown from Fig. 12 that all proposed models achieved the best results in small time steps and HRN performed more efficiently than other models.
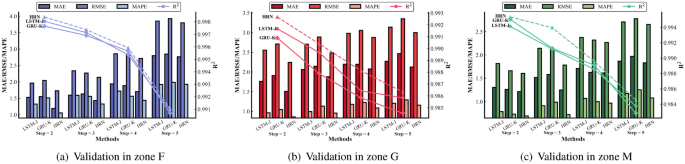
Validation of time step for different models in three zones.
The second validation is to examine the interactions of epoch and batch size on the training loss of the model. Here we set the batch size to {16, 32, 64, 128, 256} to study the loss of LSTM-J, GRU-K and HRN depending on the epoch up to 200. Figure 13 shows the test results for three experimental zones. To focus on the epoch x-axis, all numbers show that the loss could be convergent after the 50th epoch. To pay attention to the Y-axis of batch size, Fig. 13a–c show that minimal losses could be achieved at relatively small batch sizes (approximately 32) for Zone F, while Fig. 13d–i shows that minimal losses are achieved were able to produce relatively large batch sizes (approx. 128) for zones G and M.
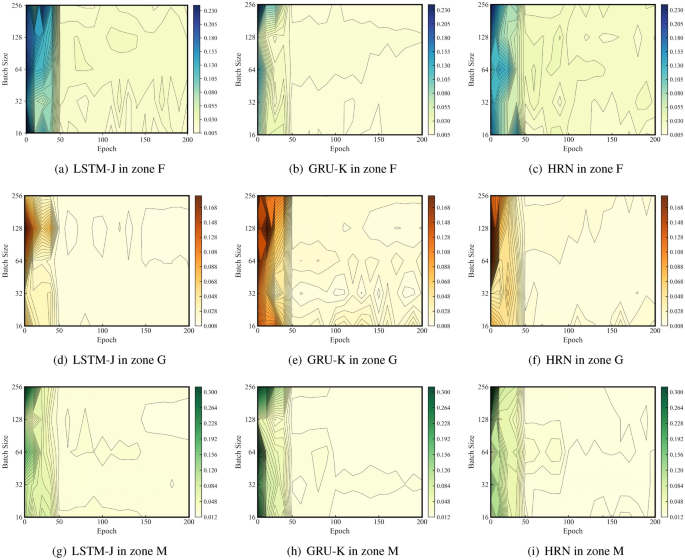
Validation of epoch and batch size for different models in three zones.
Model complexity and performance analysis
In this section, we comprehensively compared the complexity and performance of our proposed recurrent neural network models (e.g., LSTM-J, GRU-K, and HRN) with various baseline methods. Model complexity was measured by the number of training parameters, while performance was evaluated by computation time, as shown in Table 5. Compared to traditional regression models (e.g. SVM, MLP, BPNN, RNN), our models have a slightly higher complexity in terms of computing time, but provide significantly improved prediction accuracy. Compared to existing gated architectures (e.g. LSTM, GRU, BiLSTM, CNN-LSTM), our three models have comparable complexity and computation time. In particular, compared to SOTA models (e.g. Seq2Seq, ST-LSTM and ResLSTM), our models – especially the HRN variant – offer a slight advantage in terms of complexity and computation time, but achieve almost the highest prediction accuracy and thus demonstrate a exceptional performance.